What's the problem?
The Parabolic Constant Mystery
Where is the Parabola?
The Parabolic Constant Mystery

Manas Shetty, Prajwal DSouza, Sparsha Kumari, Vinton Adrian Rebello

Our work presented here is profoundly inspired by the captivating mathematical explorations showcased in 3Blue1Brown's videos. Our specific inspiration stems from intriguing problems addressed by the channel, especially those related to the surprising appearances of pi in unexpected contexts, prompting a quest to unearth an elegant geometric connections in other problems. One particular instance that intrigued us was a connection between parabolas and squares.

This curiosity led us on an eight-month-long intellectual journey of exploring various techniques to decipher this puzzle. The discovery of a simple yet elegant connection was nothing short of a revelation that left us awestruck.

Having patiently waited for nearly three years, we believe the time is ripe to unveil our findings. It is our honor to present this work at SOME3, which we deem to be the perfect stage. As participants in SOME3, we are thrilled to share our results and be part of SOME3.

This was made with viewX , a visualization library designed specifically to make mathematical animations found on this website. It is still in developmental stage and little buggy. :)

Also, we cannot forget role of interesting ideas from Matt's video - 'There is only One True Parabola' (Standup Math) that 'all parabolas are similar' which helped us understand the concept of similarities and the nature of constants like pi.

Let us start with a innocent looking problem. Picture a unit square and pick a point Q at random along the square's boundary. What do you think is the average distance between this chosen point Q and the very heart of our square, the center C?

The average distance is the typical or middle value obtained when you add up all the distances between any two points then divide by the number of distances you added together. It's a way of finding a 'common' or 'usual' distance in a group of different distances.

Surprisingly, the answer is approximately 0.5738967... a peculiar figure, isn't it? This number equals P/4 where P is known as Universal Parabolic Constant. The value is around 2.295587149... Hold on a second - a "Parabolic" Constant? But our question was about squares, wasn't it? Where does the parabola come in?

This might seem like a co-incidence. But, we look for a circle when π pops up in various places right? Just check 3B1B :P So, why not dig a little deeper. And if we explore a little more, there are other seemingly unrelated math problems where you see this number show up.

So, What do you think is the average distance between any two points inside a unit square? Take a guess. :D

Move the slider to choose your answer... and also, the points A and B above are draggable. :)

Check
Continue

It is about 0.52140. To be more precise, it is.

$$\color{#e3a0cd}{8\left(0.0416{\color{#ffffff}{P}}-0.030473\right)}$$
And exactly, it is

$$\color{#e3a0cd}{8\left(\frac{\color{#ffffff}{P}}{24}-\frac{\sqrt{2}}{30}+\frac{1}{60}\right)}$$

Yep. Strange combination of numbers. But, there's a P there. :)
There's many more instances where we see this. But, mostly involving a unit square.

Center-Point Distance
Corner-Perimeter Distance

Center-Point Distance
Corner-Perimeter Distance

Here is a slightly similar problem.
What do you think is the average distance between the center and any point 'inside' the unit square?

Take a guess. :D

Point B above is draggable. :)

Check
Continue

It is about 0.38259785 ... To be exact, it is.

\(\color{#e3a0cd}{\frac{\color{#ffffff}{P}}{6}}\)

Yep. There's a P here too.

Let's branch out a little and delve into a problem unrelated to the unit square. A problem related to Shrinking Random Walk appeared in Tom Yuster's April 2017 Math Horizons piece (pp. 32-33)

Consider a drunkard walking in a plane that starts at the origin and moves only in the east and north directions. He randomly chooses a direction and takes a step. The walk is such that the length of the first step must be √2, the length of the second step must be √2/2, the length of the third step must be √2/4, and so on.

There are infinitely many steps. But, you can choose how many steps to show. :)

Imagine the endless steps taken by the drunkard, how far would you expect to be from the starting point, the origin?
Let's denote this distance as D.

But, here's the main question : What is the average value of D?

How could we possibly calculate that?
This problem might seem to be a departure from our discussion about the unit square. Still, it maintains a common thread: the concept of averages. (Note that the length of the path is √2 + √2/2 + ... , and we are not referring to that)

So, how about we roll up our sleeves and crunch some numbers? Let's simulate the drunkard's Walk, taking about 30 steps, and observe where we end up (roughly, and also, the length of steps beyond 8 steps is quite small to make a huge difference in final destination of the drunkard). From there, we can compute the distance, D, from the origin. To get an approximation of D's average value, we'll repeat this process a few times.

Add another trial

After looking at these values, what do you think is the average value?


Check
Continue

The answer is 2.295587149... Yes. It is P. It's here too.
This problem doesn't seem to have a square, but still deals with concept of averages.

But, why? What does this have to do with the parabola we've been discussing? Could it be connected to a concept you're already familiar with?
Here's a hint. The drunkard destination isn't that random after all. It's about the final point after large iterations . (where the drunkard lands after infinitely many steps). Let's have many trials and mark all the final positions.

Well. More trails? Move the slider. :)

Does it look familiar now? I hope we got your attention and excited about the problem.

So, what is the Universal Parabolic Constant?

Let's start with something familiar, what is pi?
If you take any circle and divide a part of it's curve, the half circumference/perimeter, by the radius of the circle, we get a value that is a constant. It's pi. This seems to be the case of parabolas too.

Circle

\(π = \frac{\text{Enclosing Arc}}{Radius}\)



= 2.2123 Parabola

\(P = \frac{\text{Enclosing Arc}}{Radius}\)



= 3.1545

Radius


In fact, the universal parabolic constant 2.295587... is an irrational number and is equal to \(√2 + ln(1+√2)\).
If we have the radius of a circle, we can compute the circumference. If you are provided with the "radius" of a parabola, we can measure the enclosing arc length..

Enclosing Arc = Universal Parabolic Constant x Radius

This is true for an asteroid's parabolic trajectory, or for a tiny parabolic satellite dish, - there's a parabola in there, with our universal parabolic constant winking back at us.

You see, these constants are the universal translators, making sense of the circles and parabolas, no matter where we find them. Whether it's a arc bridge or the edge of a penny, these constants underlie the geometry. Even the trajectory of a jet of water from a fountain, links back to these beautiful constants.

Why do these constants appear?

Can we cook up more? Are they present only in parabolas and circles? I mean.. take a square of side length \(L\) if you take a ratio of perimeter \(4L\) divided by diagonal \(\sqrt{2}L\) is always \(\frac{4}{\sqrt{2}}\).
Turns out any shape that scales symmetrically, has these constants. To be more specific, similar shapes will posses such constant... and yeah, all circles are similar. But here's a surprise, all parabolas are similar too. Please check Matt's video (Standup Math) for more details.

Because, when we scale a shape by a certain amount, let's say.. doubling the size of a circle, the radius and circumference both double. So, the ratio of circumference to radius remains the same. The same goes with any shape, the ratio of perimeter to diagonal for a square.

But what does radius and center of a parabola even mean?
First, what is a parabola?
How do we construct a parabola?
Take a fixed point F. Take a line L. Then, then pick a point Q such that the distance between this point Q and F is the same as the distance between this point Q and the line L.
Parabola is a set of points that are at the same distance from a fixed point (F), as the perpendicular distance from a fixed line (L).

Move the slider to see more points that obey the same distance rule.

Before we go ahead and tell you what Parabolic constant exactly is. lets describe the anatomy of a parabola
The fixed point is called the Focus, usually denoted F. If we go by the definition, one of the special points is the vertex of the parabola (let's say C), which has the shortest distance (let's say a) from the fixed line L. There are two more interesting points on the parabola, the ones that cut the parabola if we draw a line M parallel to the fixed line L, passing through the focus F.

The two points are G and H drawn below.

Next

This point H associated with a distance of 2a is going to be important later.
The line FH, equivalent to half the latus rectum of the parabola, is something akin to its 'radius'.
Latus rectum (GH) is sort of equivalent to the diameter and is equal to 4a.

And remember this. HB has length 'a' units and CB has length '2a' units.
For example: If HB has length 0.5 units and CB is 1 unit.

Keep in mind that arc GCH is the enclosed arc of the parabola, and the line FH can be likened to its 'radius'. With this understanding, we can see how the Universal Parabolic Constant, P, acts as the ratio of the arc GCH to FH. Thus, we can write:

Arc \(\color{#a585ff}{GCH}\color{#737373} = \color{#ffffff}P\color{#737373} \times \color{#ff7a7a}FH\)

If we rewrite the length of the enclosing arc GCH as P x 2a, then the arc CH will be P x a, we have a clear relationship between these parts of the parabola and the UPC. In other words, we find that : $$Arc \; \color{#a585ff}{CH}\color{#737373} = \color{#ffffff}P\color{#737373} \times \color{#e3a0cd}a$$ Which, substituting the value of the UPC, gives us : $$Arc \; \color{#a585ff}{CH}\color{#737373} = \color{#ffffff}2.292334..\color{#737373} \times \color{#e3a0cd}a$$

Here's another interesting property of the parabola. This might be obvious if you have encountered it in calculus, otherwise, take our word for it.

Consider the equation of a line
\(\color{#737373}{y = \color{#ffffff}{m}\color{#61bdff}{x}}\)

Taking one of the simplest parabolas, we see that
\(\color{#737373}{y = x^2 = \color{#ffffff}{x}\color{#61bdff}{x}}\)

Meaning it seems like the rise or fall (slope, to be precise) of the curve at a given point increases as you move future away from the origin along the x axis. (steepness increases with the value of x) How do we know that? Well its simple to illustrate, just draw a line that touched the curve at the point of interest, (tangent, as an arrow here) and see the steepness of this line increase with increase in the x coordinate of the point of interest.

The parabola can be thought of a curve whose slope changes (linearly) with the position of the x coordinate. Also, notice that a tangent drawn to the parabola at the point H, makes a 45 degree angle with the x axis. Or in more precise terms, the slope of the parabola at the point H (x = 2a) is 1 (corresponding to an angle of 45 degrees).

Value of the x co-ordinate

For those among you, who want a serious proof that the slope is indeed equal to 1 at point H. Here's some calculus.

The equation of the parabola, with latus rectum 2a is given by

$$y = \frac{x^2}{4a}$$

The points C and H here are at (0,0) and (2a, a) respectively.

Because when
1. \(y = 0 \) when \(x = 0 \) (the vertex C)
2. \(y = a \) when \(x = 2a \) (our point H)


Now, differentiate the equation of the parabola to get the slope at any point (x,y) on the parabola.
$$\frac{dy}{dx} = \frac{x}{2a}$$ So, at H, where x = 2a, \(dy/dx = 2a/2a\) = 1, so the slope is 1, and hence,

At H, the tangent makes a 45 degree angle with the x axis.

Moving on.

A small detour. The Division of lines.

12/4 is 3. That's simple division.
Okay, so here's a question. I have a piece of ribbon whose length is 12. Can you find a method such that I get a piece of ribbon whose length is 3?

I give you the big ribbon. Do something to this. And give me back the small ribbon.

A straightforward method?

1. Break the ribbon evenly into 4 pieces.
2. Keep one piece.

Next

This method is good. But there is another approach that might be more useful for us.

Shrinking the line segment, by a factor of 4.

Next

This method is actually a little better for curves.

How do you perform the same operation for curves? How to divide a curve of length \( L \) to get a identical curve of length \( L/n \) ? (where n is a number).
Let's start with a line..



Scaling down along both x and y by a factor of 4, will give us the line segment we want. It's length is 3.. which is 12/4.

This can be done with any curve. Let's say we take a curve of length 20. And we want to divide it by 4. But we also want to preserve the shape of the curve..




Continue

So, now you know how to divide a curve. What's next? Be patient. It will all make sense.

What is average?

The problem is about average value, right? So, what is average?

How does one calculate average?

One approach is to go through all possible cases. Add them and then divide by the number of cases. For example, What is the average value (expected value) of a die roll? $$\color{#a585ff}{A} \color{#737373}= \frac{\color{#e3a0cd}{1} \color{#4a76e5}+ \color{#e3a0cd}{2} \color{#4a76e5}+ \color{#e3a0cd}{3} \color{#4a76e5}+ \color{#e3a0cd}{4} \color{#4a76e5}+ \color{#e3a0cd}{5} \color{#4a76e5}+ \color{#e3a0cd}{6}}{\color{#ff7a7a}{6}} $$

If there are 9 people in the room, all with height 6 ft, what is the average height?

$$ \color{#a585ff}{A} \color{#737373}= \frac{ \color{#e3a0cd}6 \color{#4a76e5}+ \color{#e3a0cd}6 \color{#4a76e5}+ \color{#e3a0cd}6 \color{#4a76e5}+ \color{#e3a0cd}6 \color{#4a76e5}+ \color{#e3a0cd}6 \color{#4a76e5}+ \color{#e3a0cd}6 \color{#4a76e5}+ \color{#e3a0cd}6 \color{#4a76e5}+ \color{#e3a0cd}6 \color{#4a76e5}+ \color{#e3a0cd}6} {\color{#ff7a7a}{9}} $$

But here is something interesting.

What is the average of the following numbers?
1, 6, 2, 2, 6, 2, 1, 1, 6

If you carefully rearrange,

$$ \color{#a585ff}A \color{#737373}= \frac{\color{#ccc161}1 + 2 + 6 + \color{#adff7a}1 + 2 + 6 + \color{#ccc161}1 + 2 + 6}{\color{#ff7a7a}9} $$

the average can simply be... $$ \color{#a585ff}A \color{#737373}= \frac{ \color{#ccc161}1 + 2 + 6}{\color{#ff7a7a} 3} $$

Instead of taking the average of all 9 numbers, we can take the average of 1, 2, 6 because they repeat.
If you have 10 people with average height of 6 foot, getting 10 more identical people (whose average is obviously 6 foot because they are identical), doesn't change the average height of the total.
This is because these groups are identical, and due to symmetry, we can ignore these repeating numbers during calculations.

Average for 1, 2, 6, 1, 2, 6, 1, 2, 6
is the same as
Average for 1, 2, 6, 1, 2, 6, 1, 2, 6, 1, 2, 6, 1, 2, 6, 1, 2, 6, 1, 2, 6, 1, 2, 6, 1, 2, 6
is the same as
Average for 1, 2, 6



So, when asked, What is the average distance between a point Q on the square the center C? There is a chance to simplify the problem by re framing the question due to repetition of the points that lie on the perimeter of the square. What is the average distance between the point C and a point on the line AB?

Sounds like there is a fixed line and a fixed point. :P But, no sight of parabola yet. Wait for a while.
Let's see where this will take us in a minute or two.

The simpler problem

Now the bare bone of problem to solve is that, If there is a line of height 0.5, standing at a distance of 0.5 from point C, what is the average distance between the point C and a point on the line?

To make our calculations easier, let's lengthen the side of the square by 2, so the distance CB is 1. So, now the problem becomes : If there is a line of height 1, standing at a distance of 1 from point C, what is the average distance between the point C and a point on the line?

One approach to calculating average is to sweep through all possible cases. Add them and then divide by the number of points. If we take every single point on the line once, add the distances and divide by the number of points taken while calculating , that should work? But, how to take every single point while calculating the mean. There are infinitely many points here. Infinitely many cases.

Let's take only a few points, instances first. How about 2 points? The easy ones. A and B.

In this case, numerically the average for two lengths is

$$\color{#a585ff}A_{\color{#ff7a7a}2} \color{#737373}= \frac{ \color{#e3a0cd}CB \color{#737373}+ \color{#adff7a}CA}{\color{#ff7a7a} 2} $$

\( \color{#a585ff}A_{\color{#ff7a7a}2} \color{#737373}= \frac{ \color{#e3a0cd}1 \color{#737373}+ \color{#adff7a}\sqrt{2}}{\color{#ff7a7a} 2} \color{#737373}= \frac{ \color{#e3a0cd}1 \color{#737373}+ \color{#adff7a} 1.414..}{\color{#ff7a7a} 2} = \color{#ffffff} 1.207..\)

CA is square root of 2 by Pythagoras theorem.

Now, how about 3? If we evenly divide the line into two, we can get three points. A, B and a midpoint E.

In this case, numerically the average for three lengths is

$$ \color{#a585ff}A_{\color{#ff7a7a}3} \color{#737373}= \frac{\color{#e3a0cd}CB \color{#737373}+ \color{#e7d9b6}CE \color{#737373}+ \color{#adff7a}CA}{\color{#ff7a7a} 3} $$

\( \color{#a585ff}A_{\color{#ff7a7a}3} \color{#737373}= \frac{ \color{#e3a0cd}1 \color{#737373}+ \color{#e7d9b6}\frac{\sqrt{5}}{2}\color{#737373}+ \color{#adff7a}\sqrt{2}}{\color{#ff7a7a} 3} \color{#737373}= \frac{ \color{#e3a0cd}1 \color{#737373}+ \color{#e7d9b6}1.118.. \color{#737373}+ \color{#adff7a} 1.414..}{\color{#ff7a7a} 3} = \color{#ffffff} 1.1773..\)

CE is square root of 5 divided by 2 by Pythagoras theorem.

Our goal is to find the average distance, and we need to sweep through all instances. So.. we are trying to find \( \color{#a585ff}A_{\color{#ff7a7a}n} \) as \(n\) becomes infinity.

Now, how about 4? or 5... or n points, If we evenly divide the line into 3 parts, we can get average for 4 points. (cases)
If divided into 4 parts, we can get average for 5 points. If divided into (n - 1) parts, we can get average for n points (cases).

So, you might be asking. This looks good. Numerically, we can add all of them and then divide by the number of points. Do it for infinitely many points.
But how is this related to the parabola? Where is it?

Can you see it?

There is a parabola somewhere in there.
Let's start with the simplest approximate average, that takes just 2 points. Remember the answer to this?

Add Scale down

$$ \color{#a585ff}A_{\color{#ff7a7a}2} \color{#737373}= \frac{ \color{#e3a0cd}CB \color{#737373}+ \color{#adff7a}CA}{\color{#ff7a7a} 2} = \frac{1 \color{#ffffff}+\color{#737373} \sqrt{2}}{2} $$

How do we take average? Add and then Divide.

The first step is to add the cases lengths. How do you add CA and CB? How do you add lines?
To add, CA and CB, we can lay them next to each other. Now the whole curve, green line + pink line represents our sum.
Drag the slider to move the curve/line.

\( \color{#a585ff}A_{\color{#ff7a7a}2} \color{#737373}= \frac{ \color{#e3a0cd}CB \color{#737373}+ \color{#adff7a}CA}{\color{#ff7a7a} 2}\color{#737373} = \color{#ffffff}\frac{\color{#737373}1 + \sqrt{2}}{\color{#737373}2} \)

The next step? Divide. How do you divide a line?
Adding curves was easy. But how do we divide a curve by 2? Remember? Shrinking along both axes? Drag the slider to scale down along both x and y axes.

The length of the curve that's scaled down \( \frac{ \color{#e3a0cd}CB}{\color{#ff7a7a} 2} \color{#737373}+ \frac{\color{#adff7a}CA}{\color{#ff7a7a} 2} \)
represents the sum \( \color{#a585ff}A_{\color{#ff7a7a}2} \)

The length of this curve represents the average distance for those 2 points

Continue
Continue

This is just 2 points/cases, we need to consider more points in order to get an accurate answer. How about 3 now?

Add Scale down

\( \color{#a585ff}A_{\color{#ff7a7a}3} \color{#737373}= \frac{ \color{#e3a0cd}CB \color{#737373}+ \color{#ffbe8f}CQ \color{#737373}+ \color{#adff7a}CA}{\color{#ff7a7a} 3} = \frac{1 \color{#ffffff}+ \color{#737373} \frac{\sqrt{5}}{2} \color{#ffffff}+\color{#737373} \sqrt{2}}{3} \)

Now, you know the drill. Add and then Divide.

The first step is to add the lengths from each case (CA, CQ and CB). Like earlier, To add, CA, CQ and CB, we can lay them next to each other. Now the whole curve, green line+ orange line + pink line represents our sum.
Drag the slider to move the curves/lines.

\( \color{#a585ff}A_{\color{#ff7a7a}3} \color{#737373}= \frac{ \color{#e3a0cd}CB \color{#737373}+ \color{#ffbe8f}CQ \color{#737373}+ \color{#adff7a}CA}{\color{#ff7a7a} 3} = \color{#ffffff} \frac{\color{#737373}1 + \frac{\sqrt{5}}{2} +\color{#737373} \sqrt{2} \color{#ffffff}}{\color{#737373} 3} \)

The next step? Divide. How do we divide a curve by 3?
Time to shrink the curve along both axes by a factor of 3. Drag the slider to scale down along both x and y axes.

The length of the curve that's scaled down \( \frac{ \color{#e3a0cd}CB}{\color{#ff7a7a} 3} \color{#737373}+ \frac{ \color{#ffbe8f}CQ}{\color{#ff7a7a} 3} \color{#737373}+ \frac{\color{#adff7a}CA}{\color{#ff7a7a} 3} \)
represents the sum \( \color{#a585ff}A_{\color{#ff7a7a}3} \)

The length of this curve represents the average distance for those 3 points.

Continue
Continue

Sounds a little familiar? Also, notice that we can scale down the curves first and then add them too. Divide each segment/case by 3 and them add them together.

$$ \frac{ \color{#e3a0cd}CB \color{#737373}+ \color{#ffbe8f}CQ \color{#737373}+ \color{#adff7a}CA}{\color{#ff7a7a} 3} $$ $$ \frac{ \color{#e3a0cd}CB}{\color{#ff7a7a} 3} \color{#737373}+ \frac{ \color{#ffbe8f}CQ}{\color{#ff7a7a} 3} \color{#737373}+ \frac{\color{#adff7a}CA}{\color{#ff7a7a} 3} $$
Let's do it the other way round now.
For 3 points, we sample 3 points. Break line into 2. Take distances to 3 points. Divide each of them by 3. Add them together.

Now, How about 4 points or more?
Sample. Break line AB into 3. Take distances to 4 points. Divide each of them by 4. Add them together.

Scale down Add

\( \color{#a585ff}A_{\color{#ff7a7a}4} \color{#737373}= \frac{ \color{#e3a0cd}CB}{\color{#ff7a7a} 4} \color{#737373}+ \frac{ \color{#ffbe8f}CQ}{\color{#ff7a7a} 4} \color{#737373}+ \frac{ \color{#ffbe8f}CK}{\color{#ff7a7a} 4} \color{#737373}+ \frac{\color{#adff7a}CA}{\color{#ff7a7a} 4} = \frac{1 \color{#ffffff}+ \color{#737373} \frac{\sqrt{10}}{3} \color{#ffffff}+ \color{#737373} \frac{\sqrt{13}}{3} \color{#ffffff}+\color{#737373} \sqrt{2}}{4} \)

In this case, we first divide each line segment by 4 and then add.

\( \color{#a585ff}A_{\color{#ff7a7a}4} \color{#737373}= \color{#ffffff} \frac{\color{#737373}1 \color{#ffffff}}{\color{#737373} 4} \color{#737373}+ \color{#ffffff} \frac{\color{#737373} \frac{\sqrt{10}}{3} \color{#ffffff}}{\color{#737373} 4} \color{#737373}+ \color{#ffffff} \frac{\color{#737373} \frac{\sqrt{13}}{3} \color{#ffffff}}{\color{#737373} 4} \color{#737373}+ \color{#ffffff} \frac{\color{#737373} \sqrt{2} \color{#ffffff}}{\color{#737373} 4} \)

Continue

Now, we add the small segments which are scaled down (CA/4, CK/4, CQ/4 and CB/4).

Like earlier, to add, CA, CK,CQ and CB, we can lay them next to each other. Now the whole curve, green line+ orange lines + pink line represents our sum.
Drag the slider to move the curves/lines.


The final curve made by scaled segments, represents our sum \( \color{#a585ff}A_{\color{#ff7a7a}4} \). Looks more familiar uh?

Continue

Starting to look familiar, uh?
So. the algorithm for 4 points was.
Sample : 4 points, by breaking the line into 3 pieces.
Divide : Divide each segment by 4.
Add : Add the 4 segments together by laying them together.


Now.. let's do this for n points. Sample : n points, by breaking the line into n - 1 pieces.
Divide : Divide each segment by n.
Add : Add the n segments together by laying them together.

Scale down Add

\( \color{#a585ff}A_{\color{#ff7a7a}n} \color{#737373}= \frac{ \color{#e3a0cd}CB}{\color{#ff7a7a} n} \color{#737373}+ \frac{ \color{#ffbe8f}CQ_1}{\color{#ff7a7a} n} \color{#737373}+ ... \color{#737373}+ \frac{\color{#adff7a}CA}{\color{#ff7a7a} n} = \frac{1 \color{#ffffff}+ ... +\color{#737373} \sqrt{2}}{n} \)
\( \color{#a585ff}A_{\color{#ff7a7a}n} \color{#737373} = \frac{ \color{#e3a0cd}CB}{\color{#ff7a7a} n} \color{#737373}+ \frac{ \color{#ffbe8f}CQ_1}{\color{#ff7a7a} n} \color{#737373}+ ... \color{#737373}+ \frac{\color{#adff7a}CA}{\color{#ff7a7a} n} \)

\(= \color{#737373} \frac{1 \color{#ffffff}+ ... +\color{#737373} \sqrt{2}}{n} \)


In this case, we first divide each line segment by n and then add them.

\( \color{#a585ff}A_{\color{#ff7a7a}n} \color{#737373}= \color{#ffffff} \frac{\color{#737373}1 \color{#ffffff}}{\color{#737373} n} \color{#737373}+ \color{#ffffff} \frac{\color{#737373} \sqrt{1 + {(\frac{1}{n})}^2} \color{#ffffff}}{\color{#737373} n} \color{#737373}+ \color{#ffffff} \frac{\color{#737373} \sqrt{1 + {(\frac{2}{n})}^2} \color{#ffffff}}{\color{#737373} n} \color{#737373}+ ...+ \color{#ffffff} \frac{\color{#737373} \sqrt{2} \color{#ffffff}}{\color{#737373} n} \)

$$ \color{#a585ff}A_{\color{#ff7a7a}n} \color{#737373} = $$ $$ \color{#ffffff} \frac{\color{#737373}1 \color{#ffffff}}{\color{#737373} n} \color{#737373}+ \color{#ffffff} \frac{\color{#737373} \sqrt{1 + {(\frac{1}{n})}^2} \color{#ffffff}}{\color{#737373} n} $$ $$ \color{#737373}+ \color{#ffffff} \frac{\color{#737373} \sqrt{1 + {(\frac{2}{n})}^2} \color{#ffffff}}{\color{#737373} n} \color{#737373}+ ...+ \color{#ffffff} \frac{\color{#737373} \sqrt{2} \color{#ffffff}}{\color{#737373} n} $$

Continue

Now, we add the small segments which are scaled down.

Like earlier, to add, CA, CQ2, CQ3,CQ4, ... and CB, we can lay them next to each other. Now the whole curve, green line+ orange lines + pink lines represents our sum.
Drag the slider to move the curves/lines.
Notice that the final point always lands at the midpoint of line AB.


The final curve made by scaled segments, represents our sum \( \color{#a585ff}A_{\color{#ff7a7a}n} \).

With many points it's beginning to look like something uh? Say it with us. It's a Parabola!. :P

At infinitely many points, this should be a parabola.

Continue

Well. It's a Parabola. :P

Wait. Back up, before that..

How do we know that it is a Parabola for sure?

If we look at the final curve, it must obey the equation of a parabola, which is

$$ y = \frac{x^2}{4a} $$ the point that obeys this equation is of the form, $$ \left(x, \frac{x^2}{4a}\right) $$

The goal is to show that if I pick any point on that curve, when we sample large number of points (that is \( n \to \infty \) ). It must obey that equation.

Let's start simple, if we had just picked 3 points, n = 3. Then, each line segment (CQ1, CQ2 and CQ3) added to the curve would contribute a point when scaled down.

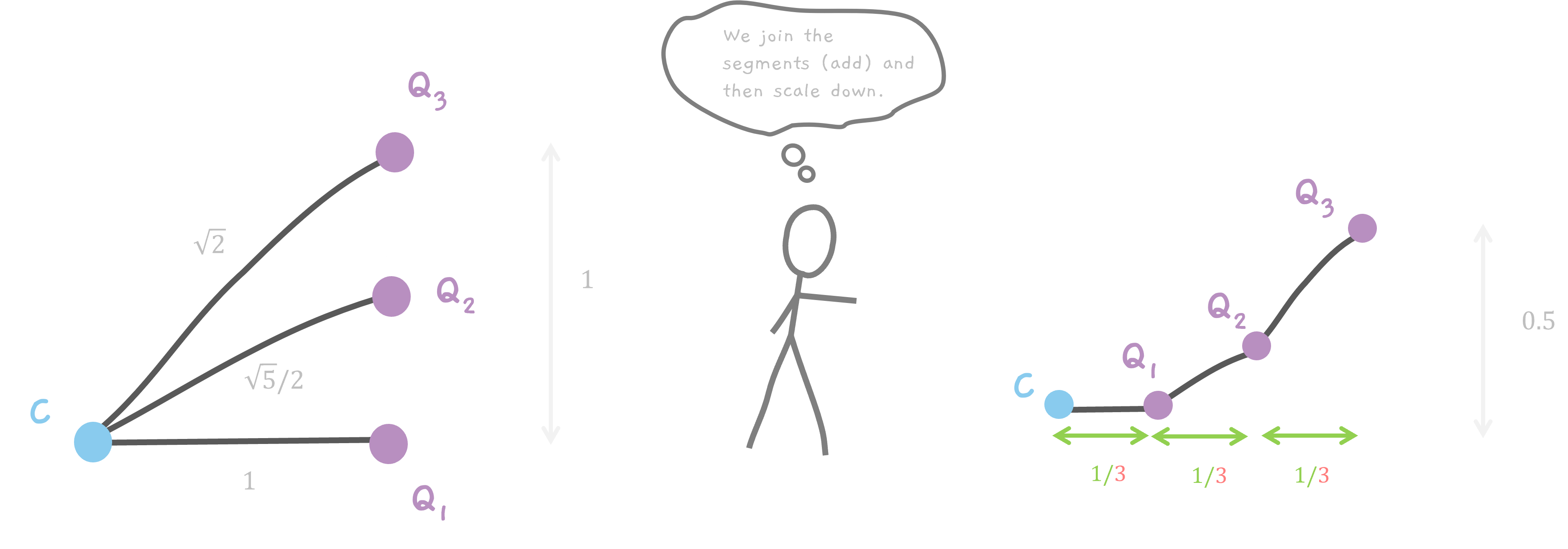
What we want is the final coordinates of the point Q1, Q2 and Q3. This is easy to do. And yes, C is the origin.
There are two steps here. Add and Scale down. So.. any point Q will hold different coordinates in each of these changes.

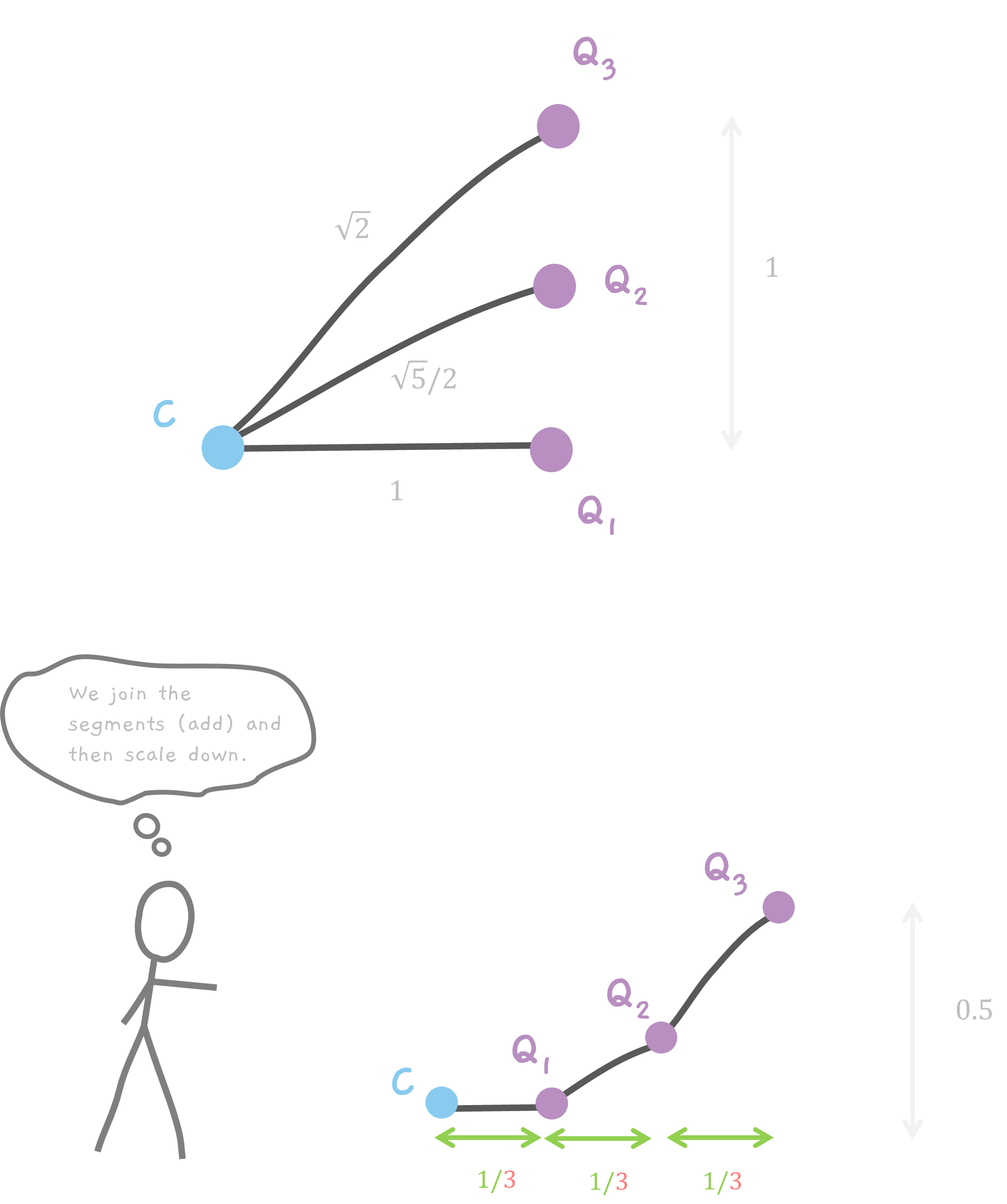
Before Adding the segments.
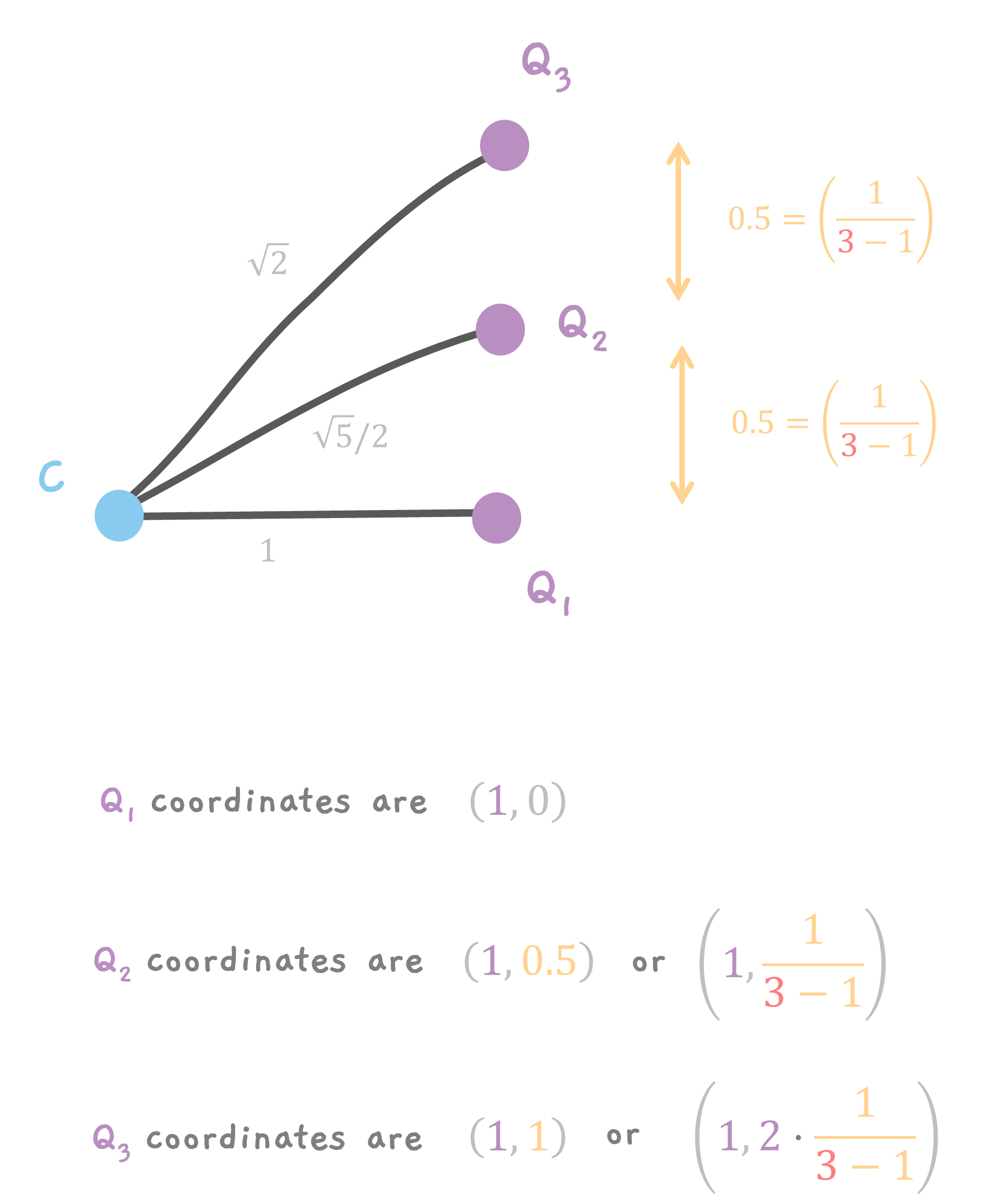
All the points are on the line AB. So, the x coordinate of all the points is 1. The y coordinate, is a fraction of the length of the line AB. Remember, for n points, we divide the line into n - 1 segments. So, the length of each segment is 1/(n - 1). So, for 3 points, the distance between each point is 1/(3 - 1) which is 1/2.
So,Q1 has coordinates of (1, 0), Q2 has coordinates of (1, 0.5) and finally Q3 has (1, 1).

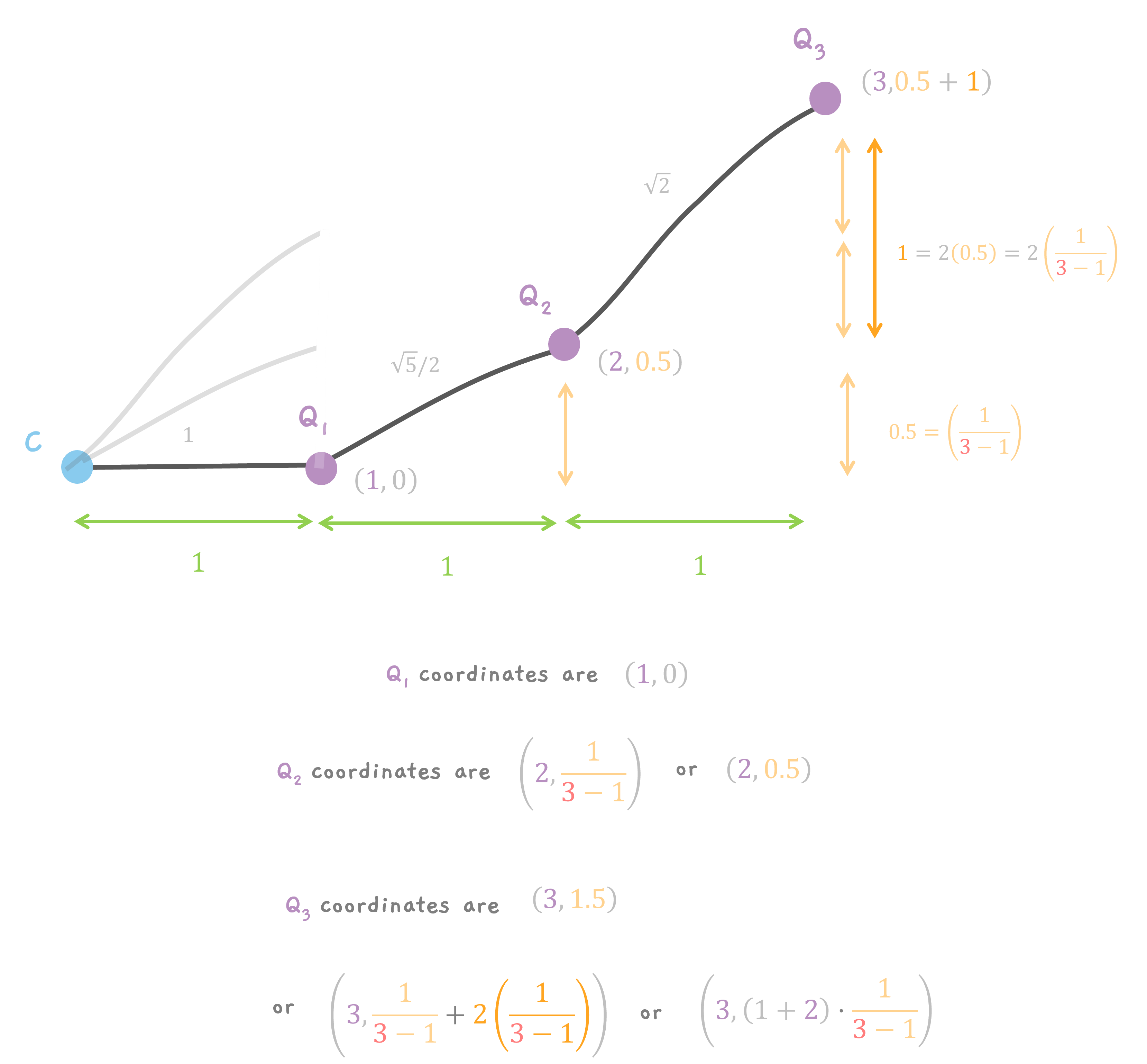
On Adding the segments.
When the segments are added and moved, the x and y coordinates change. For x coordinates, it is easy. Every point, moves to a multiple of 1. So, Q1 stays at x = 1. Q2 moves to x = 2 and Q3 moves to x = 3.
For y coordinates, it is a little more complicated.
Q1 remains where it is at y = 0. But Q2 gets a one multiple of half So, it moves to y = 0.5. And Q3 gets a two multiple of half which is 1 from earlier (remember Q3 was at a height of 1). But, also the additional 0.5 from the previous Q2 because of addition, giving y = 0.5 + 1 = 1.5.

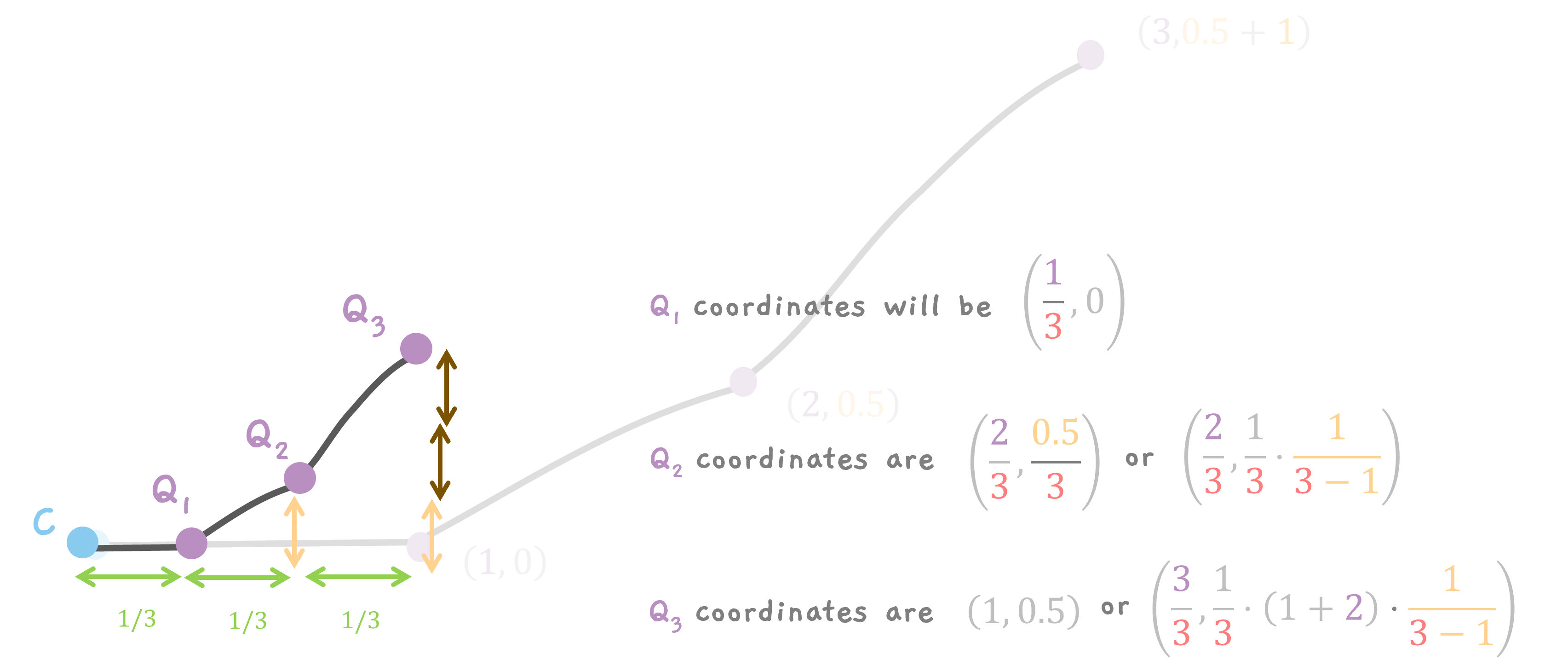
After Scaling down.
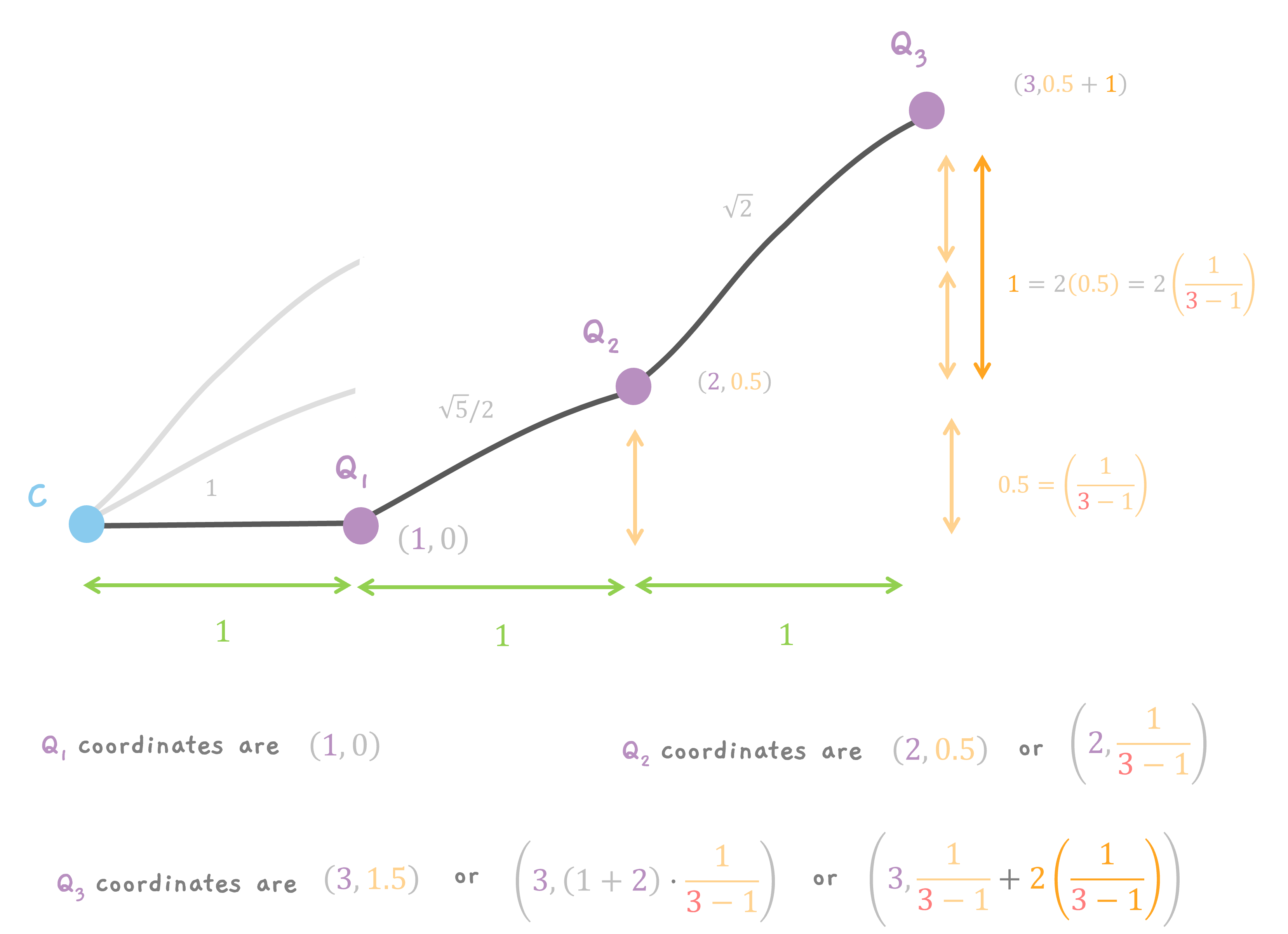
Now, we scale down the curve by a factor of 3. So, the x coordinates of all the points are divided by 3. So, Q1 goes to x = 1/3. Q2 moves to x = 2/3 and Q3 moves to x = 3/3 = 1.
The same happens to y coordinates from earlier. Q1 goes from y = 0 to y = 0/3 = 0 (I mean, stays along y). Q2 goes from y = 0.5 to y = 0.5/3. And Q3 goes from y = 1.5 to y = 1.5/3 = 0.5.
In more jargon, there is a pattern and the final coordinates look like this.

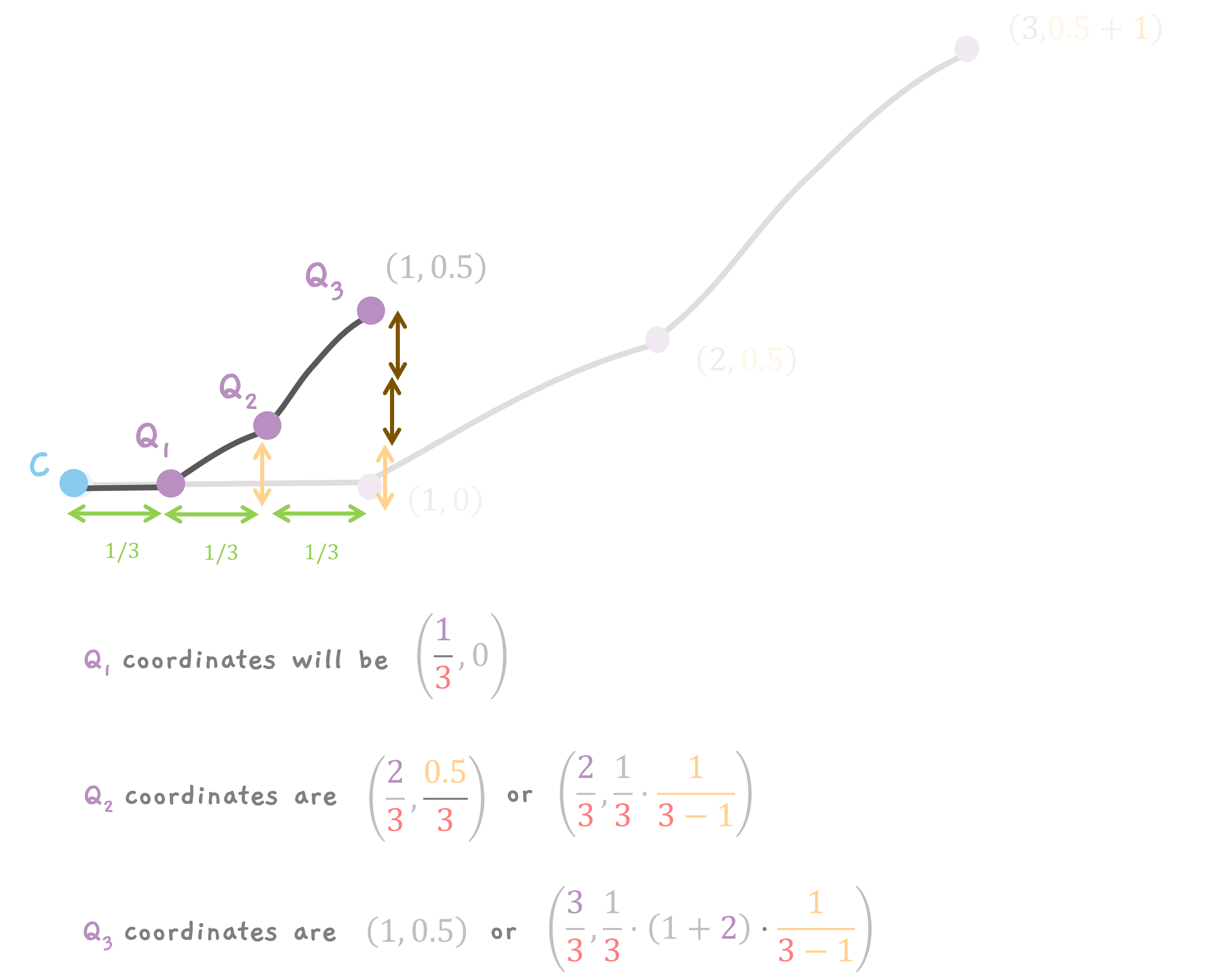
Q1, the 1st point is at (1/3, 0).
Q2, the 2nd point is at (2/3, 0.5/3) or
$$ \left( \frac{2}{3}, \frac{1}{3}\cdot (1) \cdot \frac{1}{3 - 1} \right) $$ and Q3, the 3rd point is at (1, 0.5) or (3/3, 1.5/3) or
$$ \left( \frac{3}{3}, \frac{1}{3}\cdot (1 + 2) \cdot \frac{1}{3 - 1} \right) $$


There is a pattern here and we can say that if n was 4, (this is, we sampled 4 points and divided the main line AB into 3 segments)

For n = 4, Q1, the 1st point is at (1/4, 0).
Q2, the 2nd point is at (2/4, 0.33/4) or
$$ \left( \frac{2}{4}, \frac{1}{4}\cdot (1) \cdot \frac{1}{4 - 1} \right) $$
Q3, the 3rd point is at (3/4, 1/4) or
$$ \left( \frac{3}{4}, \frac{1}{4}\cdot (1 + 2) \cdot \frac{1}{4 - 1} \right) $$ and Q4, the 4th point (final point) is at (1, 0.5) or (4/4, 2/4) or
$$ \left( \frac{4}{4}, \frac{1}{4}\cdot (1 + 2 + 3) \cdot \frac{1}{4 - 1} \right) $$

In general for n = 4,
The kth point, Qk is at
$$ \left( \frac{k}{4}, \frac{1}{4}\cdot (1 + 2 + .. + (k - 1)) \cdot \frac{1}{4 - 1} \right) $$

And one can verify that for any n,
The kth point, Qk is at
$$ \left( \frac{k}{n}, \frac{1}{n} \cdot (1 + 2 + .. + (k - 1)) \cdot \frac{1}{n - 1} \right) $$ which can be simplified to sum of k - 1 terms to be (k - 1)k/2, hence, $$ \left( \frac{k}{n}, \frac{1}{n} \cdot \left(\frac{(k - 1)k}{2}\right) \cdot \frac{1}{n - 1} \right) $$ So, on simplifying, When we sample n points, the kth point, Qk is at
$$ \left( \frac{k}{n}, \frac{1}{2} \cdot \frac{k}{n} \cdot \frac{k - 1}{n - 1} \right) $$ Now, it should make sense, why the final point is always at y = 0.5, for the nth point, $$ \left( \frac{n}{n}, \frac{1}{2} \cdot \frac{n}{n} \cdot \frac{n - 1}{n - 1} \right) $$ giving us, $$ \left( 1, 0.5 \right) $$

What we care about is if when we sample large number of points (that is \( n \to \infty \) ), the points, obey the equation of the parabola.

I think, we can agree that, when \( n \to \infty \) $$ \frac{k - 1}{n - 1} \thickapprox \frac{k}{n} $$ So, when \( n \to \infty \), the kth point is given by, $$ \left( \frac{k}{n}, \frac{1}{2} \cdot \frac{k}{n} \cdot \frac{k}{n} \right) $$ or $$ \left( \frac{k}{n}, \frac{1}{2} \cdot \left(\frac{k}{n}\right)^2 \right) $$ if we take x = k/n, then $$ \left(x, \frac{1}{2} \cdot \left(x\right)^2 \right) $$ or $$ \left(x, \frac{x^2}{4 \cdot 0.5} \right) $$ which is what we wanted. IT IS A PARABOLA! :D

And... this gives us \( a = 0.5. \) Yay! :D

Also, since a = 0.5, the point H is always at (2a, a), so the final point is the point H at (1, 0.5).

Wait. Back up, before that..

How do we know that the final point, always lands at the midpoint of AB?

X coordinate of the midpoint.
Let's just look at our adding and dividing curves operation.

First Adding. When we place the curves next to each other, each segment spans 1 unit in the x direction. Hence, the unscaled (scaled down) version of the curve spans n units in the x direction.
When it was 2 points, it spans 2 units in the x direction. When it was 3 points, it spans 3 units in the x direction. So, when it is n points, it spans n units in the x direction.

When we scale down by a factor n, the x coordinate of the final point should be 1 which is that of line AB here.

Y coordinate of the midpoint.
Again, similar operation.

First Adding. When we place the curves next to each other, the unscaled (scaled down) version of the curve spans different lengths in the y direction.
In the case of 2 points, the basic segment CB spans 0 units, CA spans 1 unit. And hence, totally spanning 0 + 1 units in the y direction.
(which when scaled down by 2... gave us 0.5, the midpoint of line AB)

In the case of 3 points, the basic segment CB spans 0 units, CQ1 spans 1/2 units and CA spans 1 unit. And hence, totally spanning 0 + (1/2) + 1 units = 1.5 in the y direction.
(which when scaled down by 3... gave us 0.5, the midpoint of line AB)

In the case of n points, the basic segment CB spans 0 units, CQ1 spans 1/(n - 1) units, CQ2 spans 2/(n - 1) units and soon on, with the final segment, CA spanning 1 unit.

And hence, totally spanning

\(S = 0 + \frac{1}{n - 1} + \frac{2}{n - 1} + \frac{3}{n - 1} + ... + \frac{n - 2}{n - 1} + \frac{n - 1}{n - 1} \)

\( = \frac{1}{n - 1}(1 + 2 + 3 + ... + (n - 2) + (n - 1)) \)

Since, Sum of natural numbers upto n is \(\frac{n(n + 1)}{2}\)

Sum of natural numbers upto n - 1 is \(\frac{(n - 1)(n - 1 + 1)}{2} = \frac{(n - 1)(n)}{2}\)

substituting that,

\(S = \frac{1}{n - 1}(\frac{(n - 1)(n)}{2}) \)

\(= (\frac{n}{2}) \)

So, now we know that it spans n/2 in the y direction when added (unscaled) for n points. (That is... for 2 points its 2/2.. and 3 points it is 3/2 as we saw earlier)

So, when scaled down by a factor of n.. n/2 scales down to 1/2.

Making the y coordinate of the final point in the curve to be 1/2, which is that of line AB.

There are characteristics to look for that show that it is a parabola.

The last segment (corresponding to unscaled CA) added to the curve which is currently at the midpoint is always at the 45 degree angle. Each segment increases it's slope linearly. Reminds me of some familiar curve.
The midpoint on the line segment AB, could be our point of interest H? (Yes, it is, as proven in the previous sub section. :P)


Also, remember this?
HB has length a units then, CB has length 2a units.
HB is a and CB is 2a. If HB is 0.5 and CB is 1.
CB is indeed 1 here and midpoint H of AB (length 1), hence HB = 0.5.


If this is the Parabola (Yes, it is, as proven in the previous sub section. :P) and the curve indeed always lands at the midpoint H of AB,
Remember?
Arc \(\color{#a585ff}{CH}\color{#737373} = \color{#ffffff}P\color{#737373} \times \color{#e3a0cd}a\)
Then, the length of the arc CH in our parabola is P times a, where a is the distance HB, which equals 0.5 in our case.
Arc \(\color{#a585ff}{CH}\color{#737373} = \color{#ffffff}P\color{#737373} \times \color{#e3a0cd}0.5\)
So, our calculated average, represented by

Arc \(\color{#a585ff}{CH}\color{#737373} = \frac{\color{#ffffff}P\color{#737373}}{\color{#e3a0cd}2}\)


Wait. That's doesn't seem right.
What we wanted was \(P/4\) , not \(P/2\)

This is due to the scale of our square - its side length is 2. The original problem has a side length of 1.
If we considered a square of side length 1, where CB equals 1/2 and hence, HB (or a), equals 1/4, then for this square,
Arc \(\color{#a585ff}{CH}\color{#737373} = \color{#ffffff}P\color{#737373} \times \color{#e3a0cd}\frac{1}{4}\)

Arc \(\color{#a585ff}{CH}\color{#737373} = \frac{\color{#ffffff}P\color{#737373}}{\color{#e3a0cd}4}\)

as initially calculated.


Going ahead, we can predict the average distance for any square,
For square of side 1, it is P/4 and for side 2, it is P/2.. In general, for a square whose side as length L, the average distance between it's center and a point on it's perimeter is

\(\color{#ffffff}\frac{P}{4}\color{#737373} \times \color{#e3a0cd}L\)



In summary, we began with an apparently innocent problem concerning the average distance in a unit square and the unrelated issue of a drunkard's random walk. Intriguingly, we demonstrated their equivalence.

The Universal Parabolic Constant (UPC), which cropped up consistently, led us tackle this through the geometric proof . We employed the idea of geometric averages and examined points on a line, calculating the lengths between the center and sampled points. By laying these line segments side by side and scaling down the resulting curve proportionally to the number of points sampled, a parabola astonishingly emerged.

Through this exploration, we hoped to show how the study of mathematics is not about isolated concepts, but an interconnected symphony of ideas.